「マックスウェル・ボルツマン分布」（１）
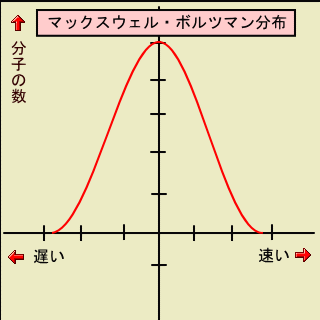
右にあるグラフは「マックスウェル・ボルツマン分布」と呼ばれるもので、波型の曲線は一定温度での気体分子の速度の分布を表している。縦軸は「気体の分子の数」であり、横軸は「気体分子の速度」で右にゆくほど速くなっている。このマックスウェル・ボルツマン分布は、「最も平均的な速度を持つ分子の数が最も多い」ことを示すグラフであり、「平均からずれればずれるほど、その数は少なくなる」ことも示している。そして、「平均から遠く離れたものも数は非常に少ないが、ないわけではない」ことも示しているのである。つまりこの宇宙では「最も平均的なことが最も数多く起こり、平均からずれるようなことは、平均からずれればずれるほどその数は少なくなり、平均から遠く離れたようなことも、数は少ないが起こらないわけではない。」ということだ。これがこの「宇宙」で起こる全ての現象の基本であり理想であると、私は考えている。
なぜそのように考えられるのか？ それはこの分布に見られる相関が、「全く同じルール」によって制限された「全く同じ自由」と「全く同じエネルギー」を持つものを「全体的」な視野から見た「ルール」だからである。また、この分布が「宇宙の安定性と新奇性」という相反する二つの局面を見事に物語っているからである。
この宇宙で実際に起こる「現象」の全てを、深くそして正しく理解するには、この「MB分布」（これからはマックスウェル・ボルツマン分布のことをこう書く事にする。面倒だから。）について、考察するのが最も良いのである。人間が、この宇宙で起こる現象について少なからず持っている誤解と、その誤解ゆえに人間自らが引き起こしている、この宇宙にふさわしくない「現象」についても理解してもらえると思う。ではまず、なぜ「MB分布」がこの宇宙にある全ての現象を表すグラフなのか、その根拠について書いてゆくことにしよう。
物理学では「固体」のことを長距離秩序のあるもの、「液体」のことを短距離秩序のあるもの、「気体」のことを秩序のないものと言う。だから個々の「気体分子」は、全くデタラメに飛び回っていて、その運動は「ブラウン運動」（不規則な運動）と呼ばれて「秩序のないもの」である。だが、個々の気体分子の運動はデタラメでも、気体分子の一つ一つが何の「ルール」にも従っていないかというと、そんなことはなくて、ちゃんと「物理法則」には従っている。一つ一つの「気体分子」は「物理法則」によって組み立てられたものであるし、それらが衝突するときには、ニュートン博士の「運動の法則」に従っているし、各種の「保存則」もきちんと守られている。にもかかわらず、個々の「気体分子」の運動は全く「デタラメ」であり、その運動からは一つの「ルール」も見出すことはできないのだ。奇妙な話だ。だが、そんな気体分子も１０の２３乗個ほど集まった「全体」として観察すると「ルール」が見えてくると言うのが「MB分布」である。気体の分子一つ一つは全く同じものであり、全く同じルールによって制限されている。また元あったエネルギーも同じである。だが、それらが衝突を繰り返すたびに「速度」は変化する。気体分子の運動はデタラメだから、一つ一つの分子どうしが、どの角度でどれぐらいの速度でぶつかるのかはわからない。だから一つ一つの分子の速度も飛んで行く方向もデタラメである。だが、そんな気体分子の運動を「全体」として見てみたら、こんなに美しい相関が現れるのである。最も平均的な速度を持つ分子の数が最も多く、平均からずれればずれるほど、そのような速度を持つ分子の数は少なくなり、平均から遠く離れたものも数は非常に少ないが、ないわけではない という「ルール」が出現するのである。
さて、この奇妙な事実を深く理解するには、この宇宙を理解するのに絶対必要なある概念を理解しなくてはならない。それは「部分」と「全体」と呼ばれるものである。実は、物理学者が自然の中に見つけた「物理法則」には二つの「ルール」の体系がある。一つは全ての物理的な対象であるモノを「部分」を持たないモノとして扱った時にだけ有効な「全体」に関する「ルール」であり、これは一般的にはモノの「諸性質」と呼ばれるものである。例をあげよう。分子は原子でできていて、原子は素粒子でできているのだが、私たちが「分子の性質」という時には、分子の持つ「部分」である原子や素粒子の性質は無視される。つまり「分子」を一つの「全体」として見たときにだけ、「分子の性質」ということが言えることになる。太陽も地球も月も、分子や原子で出来ているのはわかっているが、それぞれの星の「性質」について述べる時には、「部分」であるものの性質などは無視されている。だから「諸性質」は常に「部分」を持たないモノとして、「全体」として扱った時にだけ語ることができるものである。
もう一つは全ての物理的な対象を「部分」を持たない「全体」として扱った時に、その「全体」どうしの間にある「ルール」である。ただし、この「ルール」を私たち人間が知っていることの有効性は、基本的に「全体」の数がたったの「二個」の時に最大となり、数が増えるに連れて薄れてゆく。つまり、「全体」の間にある「ルール」は、その「ルール」に関わる「全体」の数が「二個」の場合は厳密に理解できるが、三個、四個と数が増えてゆくと、わからなくなってゆくということである。例をあげよう。太陽系の中にある惑星が地球だけであり、太陽と地球の運動を理解しようとすれば、高い精度で理解できる。この二つの星の間には「万有引力の法則」という「ルール」があって、私たちはその「ルール」が高い精度で確実であることを知っているのだから、それに従っている二つの星の「運動」を高い精度で理解できるのは当然のことである。この二つの間にある「万有引力の法則」はたった一つの方程式で表すことができる。だが、地球の周りには衛星としての月があるし、地球の内側には二つの惑星があり、外側には５つの惑星がある。これら全てとの間に「万有引力の法則」は働いているから、一つの方程式が連立方程式になるのは当然のことだ。そして、連立方程式の数が多くなると、厳密に「解」を求めることが難しくなる。物理学者は「摂動」と呼ばれる数学的な手法を用いて、できるだけ正確な「解」に近い答えを見つけようとするが、限界があるのだ。これは「複体問題」と呼ばれて、たった三つ以上の「全体」が一つの「ルール」に関係するだけでも起こってくる問題なのである。
そして、「諸性質」についても「物体間にあるルール」についても、全ての物理的対象を「部分」を持たない「全体」として理解し、発見した物理法則を「基本法則」という。だから、「基本法則」と呼ばれるものは、「部分」を持たないモノ、例え「部分」を持っていたとしてもそれを無視して「全体」として扱った時にだけ、最も高い有効性を発揮するルールなのである。だが、この宇宙にあるものは、「部分」が「基本法則」に従って集まって「全体」を作り、その「全体」が「部分」となって、また「基本法則」に従って集まってより大きな「全体」を作るということが繰り返されて出来上がっている世界である。実際にある「全体」は、どれもこれも「部分」を持っているし、「部分」の数も相当数ある。物理学者はモノをどんどん壊して行って、「全体」をより小さな「部分」に壊せば壊すほど「部分」の数は少なくなって「基本法則」は有効になってくるのだが、この世界を作っているのはみな、分子や原子の数が「アボガドロ数（６×１０の２３乗個）」程度のモノばかりである。こんなに「多数」の「部分」を持つ「全体」に対しても、基本法則は完全に成立しているのは確かなのだが、私たちが基本法則を知っていることに有効性があるかといえば、そうとは言えない「現象」もたくさん出てくるのだ。特に、「全体」として扱えないもの、扱いにくいものである「液体」や「気体」が関係する現象については、有効性がかなり薄れてくる。では、そういった「部分」を多数持った「全体」、「全体」として扱いにくい「全体」に対して、どういう手法で「ルール」を見つけるのであろうか？ それは主に「観察」という手法を用いて「ルール」を見つけ出すのである。そうして見つけ出された「ルール」を私たちは「統計則」あるいは「経験則」と呼んでいる。物理学には、「解析力学」「熱力学」「統計力学」と呼ばれる分野があるが、これらは「現象」そのものを観察することで得られた「ルール」によって、構築されている分野である。とは言え、この分野にある「ルール」が「基本法則」と無縁であるとは誰も思っていない。関連はあるが、「部分」を多数持った「全体」、一つの「全体」として扱いにくい「全体」に対しては、「統計則」や「経験則」を用いたほうが、有効性が高いのである。そして、私たちが理解できて、かつ有効性の高い「自然のルール」は常に、「部分」を持たないとして仮定した「全体」の「ルール」だけであって、「全体」の中にあると仮定した「部分」の「ルール」そのものを把握することはできないか、できても極めてその有効性は低い。投げた野球のボールの運動は把握できるし、「ルール」によってその軌道も予測できるが、そのボールを構成する分子や原子の運動は把握できないか、できても「予測できるような」有効性は余りないというわけである。
さて「MB分布」は「統計則」である。もう少し詳しく言うと、「統計則」を元にして推測された「基本法則」である。「MB分布」の対象は気体であるが、それは実在の気体ではなく人間の頭の中だけにある「理想気体」と呼ばれるものである。「理想気体」がどんなものであるかは、ここでは話さないが、全く同じ性質を持つ気体分子の一つ一つがニュートン博士の「運動の法則」にだけ従っているとして、それを１０の２３乗個ほど集めた全体として（無限に近いほど）長時間観察したとしたら得られるれるのが「MB分布」である。着目すべきは、観察の対象である気体分子には元々「差異」が全くないことである。そして、みな「全く同一のルール」に従っていることである。そういうものが、たくさん集まるとお互い衝突し合って、「個々の気体分子」の運動や速度は全くのデタラメになり、個々の「気体分子」には「速度」の「差異」が生まれる。そして、それを全体として見たら「相関」が、すなわち「ルール」が出現することである。
この宇宙で起こる現象は全て、私が今述べた通りなのである。元はみな同じである。みんな「物理法則」という全く同じルールに従っている。個々のに起きる「現象」はみなデタラメであって、それゆえ個々に起きる「現象」には「差異」がある。だがそんな「個々」に起きる「現象」を全体として見たら、「ルール」が見えてくる。どんな「ルール」かというと、
「最も平均的なことが最も数多く起こり、平均からずれるようなことは、平均からずれればずれるほどその数は少なくなり、平均から遠く離れたようなことも、数は少ないが起こらないわけではない。」というルールである。
そして、この宇宙には、二つの相反する局面がある。一つは「進化を容認できるほどの安定性」であり、もう一つは「進化することそのものである新奇性」である。この二つが両立していないと、宇宙は今のようにはならないのだ。進化ばかり、つまり「新奇性」ばかりであれば「安定性」などできないから、新しいものが生まれてもすぐに壊れてしまうだけである。だが、「安定性」だけしかないのであれば、今度は進化する余地がない。「MB分布」は、この問題を見事に解決している。最も平均的な現象が大多数起こることで「安定性」は得られて、平均から遠くにあるような現象も数は減るが起こらないわけではないことで「新奇性」を生む余地を残している。だから、私はこの相関を「この宇宙で起こる全ての現象の基本であり、理想である」と考えたわけである。
だから、この宇宙で起こる全ての「現象」の特徴は
「最も平均的なことが最も数多く起こり、平均からずれるようなことは、平均からずれればずれるほどその数は少なくなり、平均から遠く離れたようなことも、数は少ないが起こらないわけではない。」である。
それでは、このグラフの持つ深い意味について、一つづつ話してゆくことにしよう。このグラフは、基本的にはフラクタル（入れ子構造）と呼ばれる構造を持っている。このグラフのどこかを「全体」から「部分」として取り出して、その取り出した「部分」をまた新たな「全体」として観察すれば、また同じ形のグラフになるのである。例えば、１００人の学生がいて、試験を受けたら、このグラフのよ
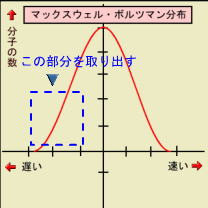うな結果になったとしよう。「平均点を取る生徒が最も多く、そこから上下に同じようなバラつきがあって、最高点の100点を取る生徒もひとりいて、最低点の０点を取る生徒もひとりいる」（このような分布であれば「中央値」と「平均値」は同じになる。）まぁ、そんなテスト結果であれば「MA分布」のようになるであろう。そこで今度は、下から３０人の学生を集めて、また新たに試験を行ったとする。そうすると、また同じようなグラフになるのである。ただし、それは「試験がいつも妥当なも
のであれば」の話しなのだが。試験が妥当であるとは、彼らの成績を測る物差しが妥当であるということだ。つまり、（前にも書いたが、「ルール」は「物差し」になるから）「ルール」が妥当であるということでもある。このグラフは、どこをどう切り取っても「ルール」さえ妥当であれば、必ずこのようなグラフになるのである。（もっともっと例を出したいが、この宇宙で起こる全ての「現象」がそうなるので、例を上げるとキリがない。だから、ここでは疑いを持っておられても構わないので、先へ進むことにする。）そして、「部分」をどんどん小さくしていって、とても小さな領域を「全体」として観察しても、また逆に、最初に観察した「現象」を含むもっとずっと大きな「現象」を「全体」として観察しても、絶対にこのようなグラフになる。どのグラフのどの場所の線も同じところには同じものがプロットされない「曲線」になっていて、絶対にグラフの線が「直線」になることはない。絶対にないのである。あっては困る。それは、この宇宙で起こる「現象」の中に「完全に同じ」があることになり、それに関わる全ての「存在」の中にも「完全に同じ」があることになるからである。この宇宙は、「完全に同じ現象」も絶対に起こさないし「完全に同じ存在」も絶対に作らない。私が、これまで「ルール」「ルール」とうるさく言ってきたから、「ルール」を尊重することで、「画一的」で「差異」のない、つまらない世界になることを心配なさる方もおられたと思うが、そんなことには決してならない。この宇宙には「全く差異のない現象」も「全く差異のない存在」も絶対に作れないメカニズムがあるからなのだ。この宇宙は、「全く同じ」が大嫌いである。「全く同じ」が大嫌いでなので、この宇宙で起こる「現象」にも、生まれてくる「存在」にも絶対に「差異」はある。私はなぜ、この宇宙が「全く同じ」を嫌っているか、その理由を知っているが、それはまたの機会にして、今はただ、このことをしっかりと理解しておいて欲しい。それは「最善のルール」「最も妥当と思われるルール」に従って「現象」が起こり「存在」が構築されたとしても、絶対に「完全に同じ」は起こらないし、生まれないし、作ることもできないということである。
夜空を見上げていただきたい。星の世界を構築し、星の世界の「現象」の全てを司っている「物理法則」は「絶対性」と「普遍性」という「法則性」を完全に持っている最上等の「ルール」であり、星の世界はそんな「ルール」だけで構築された世界である。その世界に「多様性」はないか？その世界に「個性」はないか？ とんでもない！ 全ての星はこの広い宇宙にたった一つしかないものばかりだ。その星星が織り成す全ての「現象」もまた、この宇宙でたったの一度きりしか起こらないものばかりである。この宇宙は絶対に「完全に同じ」を作らないのである。「完全性」を有する「最高」の「ルール」を全時空に敷設して、それに従って何かを作っても、みんな「個性的」で「多様性」のあるものが生まれてくるのである。
このことに関して、私たちが理解しておかなければならない大切なことがある。それはこの「MB分布」が表す「現象」を一つの「全体」として、一つの「ユニット」として考えなければならないということである。このグラフは、どんなに素晴らしいルールに従って起こった「現象」といえども、どんなに素晴らしいルールに従って構築された「存在」といえども、「平均的なもの」とその上下にばらつきのある「現象」が起こり、ばらつきのある「存在」が生まれてくることを表しているのである。つまり、どんなに頑張っても、「差異」をゼロにすることはできず、「ばらつき」をなくすこともできないということなのだ。この宇宙で起こるほとんどの現象は「平均的」なことである。だが、時にはとんでもないことも起こるのである。またこの宇宙に生まれるもののほとんどは「平均的」なものである。だが時にはとんでもないものも生まれてくるのである。「とんでもない」現象も存在も、私たちにとって「良い」方にも「悪い」方にも同程度に起こるし、生まれてくるのだ。そして、この宇宙に暮らしている私たちは、そういうものまで含むすべてを受け入れなくてはならないのである。なぜなら、このばらつきは、絶対に防ぐことができないからである。
太陽は今のこの宇宙ではとても平均的な星であり、その寿命はおよそ１００億年と言われている。だがオリオンの脇の下にあたる星「ベテルギウス」の寿命は、わずか６百万年しかない。ベテルギウスが生まれたのは、私たち人間がちょうどチンパンジーと共通の祖先から枝分かれして独自の進化を歩み始めたのと同じぐらいだから、星と言っても私たち生き物の歴史に比べてもはるかに短い寿命しか持っていない。完全性を誇る最上のルールである「物理法則」によって作られた星にさえこれだけの「差異」がある。それでも、太陽もベテルギウスも「天の川銀河」と呼ばれる一つの「全体」の中に、同じ「ユニット」の中に生まれた星なのである。
この地球に「生物」が生まれたのは、今からおよそ４２億年前のことだ。この宇宙（自然）は、地球に住む「生物構造」を確かに「秩序」の高いもの、より複雑なものへと進化させてきたのは事実であるが、それに要した時間は４２億年である。「理性」を持った私たち人間という、「自然」に比べたらとても高い「秩序」をいとも簡単に作り出す生き物を作り上げるまで４２億年もかかっているのである。そして今の私たちは、自然に比べたらとても「秩序」の高いものをごくごく当たり前にように作ることができる。それは私たちが主に、元々「秩序あるもの」である「固体」を使ってモノを作っているからであり、「QC」（クォリテイ・コントロール）という「ルール」に従って、「バラつき」を低く抑えるための「ルール」を考案してもいるし、大きな「バラつき」は排除するということもしているから、「秩序」の高いモノをたくさん作ることができるのである。そして、今や私たちの「理性」は、「宇宙のルール」「自然のルール」を把握しているのだ。そのことによって、私たちは、（自分たちに都合の良いようにではあるが）「自然淘汰」にかかる時間を「人為淘汰」によって短くし、最近では「遺伝子操作」によってあっという間に、生物に対してさも「秩序」の高いものを作る上げることができるのである。「ルールを把握」し「ルールを創造」する「理性」によって、「ルール」そのものを扱えるようになった私たち人間は、自然に比べれば猛烈なスピードで「秩序」の高いものを作ることができるのだ。だからと言って、私たち自身は、相変わらず「自然のまま」である。恐ろしいことを考えると、人間以外の有用な生き物に対しては、自分の便利のためにいとも容易く「人為淘汰」と「遺伝子操作」を行う人間であるのに、自分自身には、その制限を施し「秩序」を高めることはしていないのである。「倫理」という人間独自のルールによって今はかろうじてそれは禁止されている。それゆえ、人の「ばらつき」は自然のままなのだ。ならば、「倫理」というルールによって「ばらつき」があることを制限していないのであれば、生まれてくる人間の全てを受け入れるのが妥当であろう。オスカー・シンドラーやマザー・テレサだけを受け入れるのではなく、悪魔のような独裁者アドルフ・ヒトラーも私たちは受け入れなければならないのである。（次項に続く）
2013 all right reserved by Naniwa no Tetsugakusha